Pepsi, Coca Cola und die Geschichte der Nullhypothese
Manuel Neumann 17.06.2019
“Pepsi schmeckt gaaaanz anders!”
Wie viele gute Geschichten beginnt diese hier in einer Bar – genauer gesagt in einem Irish Pub. Die Kellnerin kommt und nimmt unsere Bestellung auf. Yannik behält die Getränkekarte anschließend einen Moment in der Hand. “Mh. Die haben hier nur Pepsi”, sagt er und löst eine Diskussion am Tisch aus: Schmeckt Pepsi besser oder schlechter als Coca Cola? Gibt es überhaupt einen Unterschied? Kann man den eindeutig feststellen? Schnell ist klar, dass sich diese Fragen im Pub nicht so schnell lösen lassen. Also einigen wir uns darauf, der Sache mit einer Verkostung bei der nächsten WG-Party auf den Grund zu gehen.
Doch die Sache lässt mich nach dem Abend auch aus einem anderen Grund nicht los: Ich erinnere mich an die Frage in einem meiner Seminare über Experimente, Wahrscheinlichkeit und statistische Methoden. Denn eine ähnliche Frage führte einmal zu einer der größten Weichenstellungen der statistischen Datenanalysen.
Wie unterscheidet man zwischen Expertise und Lüge?
Kann ich (m)einem Urteil wirklich trauen? Sagen wir, mir stellt jemand ein Glas mit einem schwarzen Erfrischungsgetränk hin, das entweder aus einer Pepsi- oder Coca-Cola-Flasche stammt, und stellt mich vor die Aufgabe, eine Aussage darüber zu treffen, um welches Getränk es sich wohl handelt. Nun kann es zwei Szenarien geben: Entweder ich bin mir nach einer Geschmacksprobe sicher, um was es sich handelt, oder ich bin es nicht und rate. Im ersten Fall gebe ich also meine Meinung kund, im zweiten sage ich zufällig Pepsi oder Coca Cola. Da ich mich aber nur einmal zwischen den beiden Marken entscheiden muss, ist die Chance, dass ich mit meiner geratenen Angabe richtig liege genau ein Halb – oder 50%.
Es ist, als würde ich einmal eine perfekte Münze werfen und danach mein Urteil fällen. Die Chance, dass ich als eigentlich völlig ahnungsloser Limo-Verkoster doch als Pepsi-Coca-Cola-Spezialist gelte, ist relativ groß. Anders ausgedrückt: Wenn ich die richtige Antwort gebe, kann die Testerin sich nicht sicher sein, ob es einen Unterschied zwischen den Marken gibt und ich den Unterschied schmecken kann.
Es braucht also mehr. Die naheliegendste Lösung ist die einfachste: Statt nur ein Glas bestimmen zu müssen, muss die Testperson die Flüssigkeit in zwei Gläsern bestimmen. Schon ganz intuitiv ist klar, dass es schwerer ist, zweimal hinereinander etwas richtig zu erraten. Und genau so ist es: Die Wahrscheinlichkeit, dass man zweimal einen richtigen Tipp abgibt, bei der jeder Tipp mit 50%-iger Wahrscheinlichkeit richtig ist, liegt bei 25%. Dies liegt daran, dass es vier mögliche Kombinationen von Pepsi und Coca Cola gibt. Entweder ist in beiden Gläsern Pepsi, in beiden Coca Cola, im ersten Pepsi und im zweiten Coca Cola, oder eben umgekehrt. Nur eine der vier Kombinationen ist aber richtig. Wählt man nun zufällig eine Kombination aus, ist diese entweder die richtige oder die falsche. Stellen wir uns vor, man würde unendlich oft raten und mit der gleichen Wahrscheinlichkeit eine der Optionen wählen, so würde man im Mittel in einem von vier Versuchen richtig liegen und damit in 25% aller Fälle. Selbst jemand ohne Geschmackssinn würde nicht immer falsch liegen. Aber die Anzahl der Fälle, in denen jemand richtig oder falsch liegt, gibt einen wichtigen Hinweis darauf, ob die Person Expertise besitzt oder lügt.
Genau so, nämlich mit Bechern voll Coca Cola und Pepsi, brachte mir mein damaliger Dozent Florian Bader die Rolle von Wahrscheinlichkeiten und das Testen von Behauptungen in der Wissenschaft näher. Woher diese Idee kommt und was sie für die Welt der Statistik bis heute bedeutet, darauf gehe ich später ein. Jetzt geht es um die eigentliche Herausforderung.
Die Challenge
Um meiner wissenschaftlichen Ausbildung gerecht zu werden muss ich die Verköstigung zu einem echten Test machen. Aber nicht mit zwei Bechern, sondern mit sechs. Um die Sache spaßiger zu machen, kaufte ich zusätzlich zu Pepsi (P) und Coca Cola (C) auch Coca Cola Zero (Z) und die ebenfalls zuckerfreie Variante der ja-Cola (J).
Die Challenge besteht aus drei Disziplinen: In der ersten gilt es, den
Unterschied zwischen Coca Cola und Pepsi zu erschmecken, in der zweiten
den Unterschied zwischen Coca Cola und Coca Cola Zero, und in der
dritten den Unterschied zwischen allen vier Cola-Sorten. Auf der Party
stellen wir drei Reihen mit je sechs Bechern auf und füllen die Becher
zufällig. Die Zufallsreihenfolge wird zuvor mithilfe einer
Zufallsfunktion in R erstellt. So ist sichergestellt, dass mehrere
Probandinnen und Probanden sich der Herausforderung stellen konnten ohne
sich gegenseitig zu beeinflussen.
Das ist eine Replikation des Codes, den ich verwendet habe:
# Challenge Nr. 1
# Die Getränke
challenge1 <- c("P", "C")
# In diesem for-loop ziehen wir drei Mal zufällige Reihenfolgen:
for (i in 1:3) {
# mit der sample() Funktion ziehen wir aus dem Objekt "challenge1"
# zufällig sechs Mal einen Buchstaben (und legen ihn nach jedem Ziehen
# wieder zurück):
reihen1 <- sample(challenge1, size = 6, replace = TRUE)
# Anschließend geben wir die Reihenfolge aus:
print(reihen1)
}
## [1] "P" "C" "C" "P" "C" "C"
## [1] "C" "C" "C" "P" "C" "P"
## [1] "C" "C" "C" "C" "P" "C"
# Und das machen wir für alle Challenges:
# Challenge Nr.2
# Die Getränke:
challenge2 <- c("C", "Z")
# Die drei Reihen:
for (i in 1:3) {
reihen2 <- sample(challenge2, size = 6, replace = TRUE)
print(reihen2)
}
## [1] "Z" "C" "Z" "Z" "C" "C"
## [1] "Z" "C" "C" "C" "Z" "C"
## [1] "C" "C" "Z" "Z" "C" "Z"
# Challenge Nr.3
# Die Getränke
challenge3 <- c("P", "C", "Z", "J")
# Die drei Reihen
for (i in 1:3) {
reihen3 <- sample(challenge3, size = 6, replace = TRUE)
print(reihen3)
}
## [1] "P" "C" "P" "P" "Z" "Z"
## [1] "J" "P" "P" "P" "P" "J"
## [1] "Z" "Z" "J" "P" "P" "J"
Die Reihen des Abends sehen so aus:
| Reihe 1 | Reihe 2 | Reihe 3 |
|---|---|---|
| CocaCola | Pepsi | Pepsi |
| CocaCola | CocaCola | CocaCola |
| Pepsi | Pepsi | CocaCola |
| Pepsi | Pepsi | Pepsi |
| CocaCola | Pepsi | CocaCola |
| CocaCola | CocaCola | CocaCola |
Für eine spätere Simulation brauchen wir eine Reihe als Objekt:
# Die Reihen der ersten Challenge:
C1_Reihe1 <- c("C", "C", "P", "P", "C", "C")
C1_Reihe1
## [1] "C" "C" "P" "P" "C" "C"
Challenge 1
Für die erste Challenge gab es vier Kandidatinnen und Kandidaten. Yannik bekam die erste Reihe, Martha und David Reihe 2, und Berkay Reihe 3. Yannik gab zwei der Becher das richtige Label, Martha vier, David fünf, und Berkay allen sechs.
Nun stehen wir vor der Frage, wer einen Unterschied zwischen den beiden Getränken ausmachen kann. Wir formulieren eine sogenannte Nullhypothese. Diese beschreibt einen Zustand der Welt, in dem das, was wir vermuten, nicht zutrifft. In diesem Falle wollen wir testen ob unsere Wettstreiter*innen einen Unterschied erschmecken konnten. Unsere Nullhypothese ist das Gegenteil: Wir gehen davon aus, dass sie keinen Unterschied schmecken können und nur raten. Wie hoch ist die Wahrscheinlichkeit, dass sie dann trotzdem die Antworten geben, die sie geben?
Die Wahrscheinlichkeit der Antworten ist davon abhängig, welche Wahrscheinlichkeit eine einzelne richtige Antwort hat und davon, wie oft man sich entscheiden muss. Daraus entsteht eine sogenannte Wahrscheinlichkeitsverteilung. Stellen wir uns vor, wir werfen eine perfekte Münze sechs Mal. Wer das zu Hause einmal versucht hat, wird feststellen, dass es weniger oft vorkommt, dass sechs Mal Kopf oder niemals Kopf vorkommt. Es kommt aber häufiger vor, dass dreimal Kopf vorkommt. Ein wenig seltener kommt vor, dass zweimal oder viermal Kopf oben liegt. Würde man diesen Münzwurf sehr oft durchführen und die Ergebnisse mit Balken in einem Diagram aufzeichnen, so hat man wenige Fälle an den Rändern (0 x Kopf, 6 x Kopf) und viele Fälle in der Mitte (3 x Kopf). Dieses Gedankenexperiment könnte man mathematisch herleiten, ich möchte diese Logik lieber mit einer Simulation darstellen.
Es wäre mühsam, 10.000 Mal sechsmal eine Münze zu werfen und die
Ergebnisse aufzuzeichnen. Noch mühsamer und teurer (und ungesund) wäre
es, gleich oft Kommiliton*innen zum Trinken von sechs Bechern Cola zu
bewegen. Zum Glück können wir uns erneut mit R behelfen und dieses
Experiment simulieren. Zuerst entscheiden wir, wie oft wir das
Experiment durchführen wollen. “Unendlich oft” brauchen wir es nicht
durchzuführen, mit 10.000 Mal sollten wir eine schöne Verteilung zu
sehen bekommen.
# Ein Objekt, das die Zahl aller gewünschten Simulationen angibt:
nsim <- 10000
Das Raten wird durch einen Zufallsmechanismus dargestellt. Nun wird 10.000 Mal eine zufällige Zusammenstellung aus Pepsi und Coca Cola erstellt. Anschließend wird automatisch abgeglichen, an wie vielen Stellen diese Zufallsreihenfolge mit der Reihe übereinstimmt, die den Wettstreitern präsentiert wird. Ich verwende als Beispiel die erst Reihe des Abends. Diese besteht aus zweimal Coca Cola, zweimal Pepsi, und wiederum zweimal Coca Cola. Der folgende Code produziert nun beispielsweise die Zufallsreihenfolge “C”, “P”, “P”, “C”, “P” und “P”. Gleichen wir die Reihenfolge nun ab sehen wir, dass die Zufallsreihenfolge an zwei Stellen richtig liegt, nämlich an der ersten und dritten. Für jedes Experiment vermerken wir die Anzahl der richtigen Treffer in einem Datensatz. (Es ist übrigens nicht wichtig, den folgenden Code zu verstehen, sondern nur, was er tut.)
# Ein leerer Datensatz, in dem die Ergebnisse eingetragen werden
simulation1 <- tibble(x = rep(NA, nsim),
Rateversuch = c(1:nsim))
# In diesem Loop passiert die Simulation:
# Wir führen den Loop 10.000 Mal durch (1 bis nsim)
for (i in c(1:nsim)) {
# Hier erstellen wir die Zufallsreihenfolge:
guess1 <- sample(c("C", "P"), 6, replace = T)
# Dann gleichen wir die Reihenfolge mit der festgelegten
# Reihenfolge ab und zählen die richtigen Treffer:
richtig <- as.numeric(C1_Reihe1 == guess1) %>% sum()
# Letztendlich tragen wir die Anzahl richtiger Treffer
# in den Datensatz ein:
simulation1[i, ] <- richtig
}
Jetzt können wir uns anschauen, wie oft unser Zufallsalgorithmus richtig geraten hat. Dies können wir tun, in dem wir die Verteilung der Fälle in einem Diagramm darstellen:
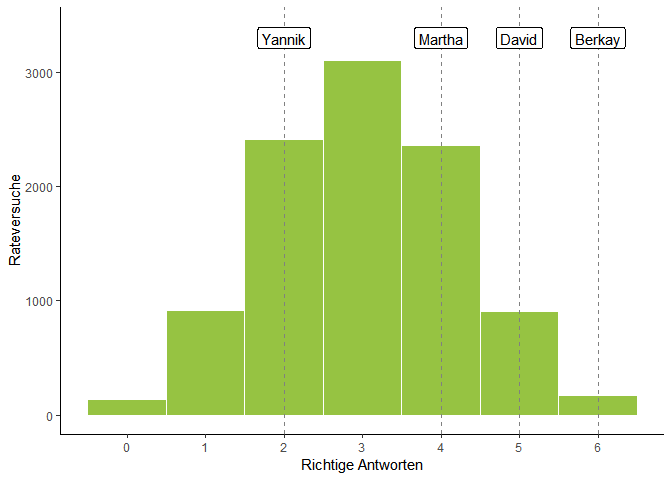 Dieses Histogramm
beschreibt die Zufallsverteilung des Experiments. Es ist klar erkennbar,
dass bei zufälligem Raten am öftesten drei Becher richtig erraten
werden. Auch wenn wir uns die Zahlen in einer Tabelle anschauen, wird
die Struktur
offensichtlich:
Dieses Histogramm
beschreibt die Zufallsverteilung des Experiments. Es ist klar erkennbar,
dass bei zufälligem Raten am öftesten drei Becher richtig erraten
werden. Auch wenn wir uns die Zahlen in einer Tabelle anschauen, wird
die Struktur
offensichtlich:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| Verteilung | 134 | 917 | 2409 | 3101 | 2360 | 907 | 172 |
| Prozentuale Verteilung | 1.3% | 9.2% | 24.1% | 31% | 23.6% | 9.1% | 1.7% |
| Aufsummierte Prozente | 1.3% | 10.5% | 34.6% | 65.6% | 89.2% | 98.3% | 100% |
In über 30% der Fälle errät selbst ein Zufallsgenerator drei Becher. In fast 78% aller Fälle werden zwischen zwei und vier Becher richtig erraten. Die Wahrscheinlichkeit, dass also Yannik und Martha keinen Unterschied geschmeckt haben und nur geraten haben, ist relativ hoch. Die Wahrscheinlichkeit, von David eine geratene Antwort gehört zu haben, liegt jedoch bei nur 10,3%. Bei ihm können wir uns wesentlich sicherer sein, dass es für ihn einen Unterschied gibt, auch wenn nicht alle seine Antworten richtig waren. Dass Berkay geraten hat, ist hingegen sehr unwahrscheinlich. In nur 1,4% aller Fälle würde er zufällig mit seinem Ergebnis richtig liegen.
Challenge 2
In der zweiten Challenge können wir die gleiche Simulation wieder zur Hand nehmen. Denn hier gilt es, Coca Cola und Coca Cola Zero auseinanderzuhalten. Nur Yannik ist dies in fünf Fällen gelungen. Eine Antwort die wir, unter der Annahme, dass er geraten hat, nur in etwas über 10% aller Fälle erwarten dürften. Die anderen können lediglich drei oder vier der Becher richtig zuweisen. Die Wahrscheinlichkeit, dass ihre Antworten auf reinem Raten beruhen, liegt erneut in dem Bereich, in dem auch 78% aller zufälligen Antworten liegen würden. Wir könnten also sagen, dass der Unterschied zwischen den beiden Sorten tatsächlich minimal sein und von den meisten wohl nicht bemerkt werden dürfte.
(Es muss natürlich angemerkt werden, dass ich hierbei immer davon ausgehe, dass die richtige Antwort gegeben werden muss. Man kann auch argumentieren, dass eine Person, die keinen Becher richtig benannt hat, alle Unterschiede geschmeckt hat, aber die zwei Marken verwechselt hat.)
Challenge 3
Spannend wird es auch bei der letzten Challenge. Hier muss der Unterschied zwischen vier Sorten erschmeckt werden: Pepsi, Coca Cola, Coca Cola Zero, und ja-Cola-Zero.
Um einen Überblick über die Verteilung der geratenen, richtigen Antworten zu bekommen, starten wir wieder unsere Simulation. Zuallererst erstellen wir eine der Reihen des Abends:
C3_Reihe1 <- c("Z", "J", "P", "P", "Z", "C")
C3_Reihe1
## [1] "Z" "J" "P" "P" "Z" "C"
Jetzt lassen wir unsere Schleife darüberlaufen und zufällig raten:
simulation2 <- tibble(x = rep(NA, nsim))
for (i in c(1:nsim)) {
guess2 <- sample(c("P", "C", "Z", "J"), 6, replace = T)
richtig2 <- sum(as.numeric(C3_Reihe1 == guess2))
simulation2[i, ] <- richtig2
}
Die Verteilung der zufällig richtig erratenen Becher sieht so aus:
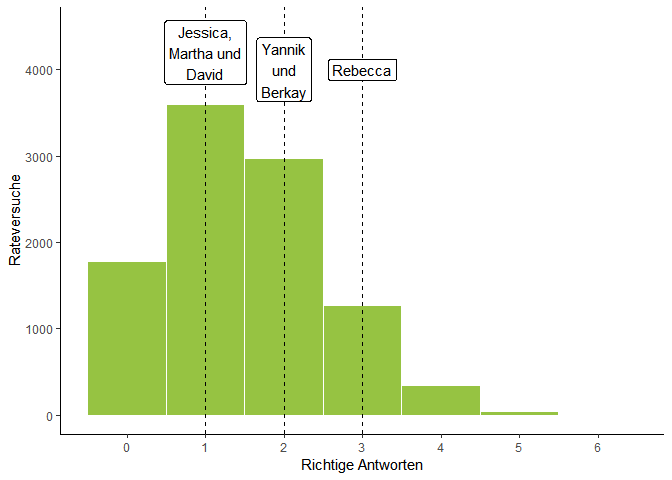
Eingezeichnet sind wieder die Ergebnisse der diesmal sechs Teilnehmer*innen. Man sieht, dass diese Challenge viel schwieriger ist. Jessica, Martha und David können einen Becher richtig bestimmen. Yannik und Berkay kommen auf zwei richtige Antworten, Rebecca auf drei. Es lohnt ein Blick auf die Verteilungen in einer Tabelle:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| Verteilung | 1777 | 3595 | 2977 | 1265 | 344 | 39 | 3 |
| Prozentuale Verteilung | 17.77% | 35.95% | 29.77% | 12.65% | 3.44% | 0.39% | 0.03% |
| Aufsummierte Prozente | 17.77% | 53.72% | 83.49% | 96.14% | 99.58% | 99.97% | 100% |
Es ist vielleicht etwas unintuitiv, aber tatsächlich ist “einmal richtig geraten” mit 35% aller Zufallstreffer der häufigste Fall. In 52% aller Fälle wird auch von einem Zufallsgenerator mindestens ein Getränk richtig erraten. Dies können auch Jessica, Martha und David. Die Chance, dass ihre Wahl ein Glückstreffer ist, ist also relativ hoch. In nur knapp 30% aller Fälle werden zwei Getränke richtig erraten. Dies ist der Fall für Berkay und Yannik. Hier wird es schwieriger zu beurteilen, ob sie immer noch nur raten, denn auch der Zufallsmechanismus errät mindestens zwei Getränke in über 83% aller Fälle.
Den besten Clou liefert Rebecca mit drei korrekten Antworten. Die Wahrscheinlichkeit von drei oder mehr richtigen Antworten liegt nur noch bei 17%. Die Wahrscheinlichkeit von vier oder mehr Richtigen bei unter 5%. Und die Wahrscheinlichkeit, alle Getränke richtig zu erraten, ist quasi Null. Der Witz ist, dass Rebecca ganz offen genau das getan hat: geraten. Eine wichtige Weisheit: Nur weil etwas unwahrscheinlich ist, bedeutet es nicht, dass der Fall nicht eintritt.
Und was hat das jetzt mit Statistik zu tun?
Und was hat das alles mit der Geschichte der Statistik zu tun?
Die Geschichte geht auf die Biologin Muriel Bristol und den Statistiker Ronald Fisher zurück. Muriel Bristol behauptete, sie könne erschmecken, ob in einen Tee Milch gegossen wurde oder ob die Milch schon in der Tasse war, als der Tee eingegossen wurde. Diese Behauptung veranlasste Fisher dazu, ein Experiment zu entwerfen, dass es erlauben würde, sie zu testen. Wie er später in seinem Buch “The Design of Experiments” schrieb, bestand der Test daraus, dass Bristol acht Tassen präsentiert wurden. In vier war die Milch vor dem Tee in der Tasse gewesen, in den vier anderen war sie anschließend eingegossen worden.
Die Neuerung war Fishers theoretische Herangehensweise. Anstatt festzulegen, wie viele Tassen Bristol identifizieren müsse, um ihr Können unter Beweis zu stellen, schlug Fisher eine sogenannte Nullhypothese vor. Diese soll den Zustand beschreiben, in dem Bristol die Tassen nicht unterscheiden kann, also nur rät. Und wenn diese unwahrscheinlich genug sei, dann könne man diese verwerfen. Es stellt sich stets die Frage: Wie wahrscheinlich ist die Beobachtung eines Zustandes (bspw. das richtige Nennen eines Getränks) unter der Annahme, dass der Effekt, der den Zustand hervorbringt, überhaupt nicht vorhanden ist (Bsp.: die Testerin weiß es nicht, sie rät). Muriel Bristol konnte tatsächlich alle Tassen identifizieren. Wie Ronald Fisher zeigte, gibt es auch für dieses Experiment eine Verteilung aller möglichen Ereignisse – so wie wir sie oben gesehen haben. Unter diesen Voraussetzungen lag die Chance, zufällig alle Tassen richtig identifiziert zu haben, bei 1,4%. Das ließ Fisher zu dem Ergebnis kommen, dass er die Hypothese, dass Bristol die behauptete Fähigkeit nicht habe, auf einem Signifikanzniveau von 1,4% zurückweisen kann.
Fazit?
Was bedeutet das für unser Coca-Cola/Pepsi-Experiment? Wir können die gleiche Logik auf die Ergebnisse anwenden (und haben das schon getan, wie vielleicht schon im Text oben aufgefallen ist). Wir können sagen, dass wir uns relativ sicher sein können, dass Berkay den Unterschied zwischen Coca Cola und Pepsi erschmecken kann. Genauer gesagt können wir die Nullhypothese “Berkay kann keinen Unterschied zwischen Coca Cola und Pepsi schmecken” und damit auch “Es gibt keinen Unterschied zwischen Coca Cola” auf einem Signifikanzniveau von < 2% zurückweisen. Für David, Yannik und Martha müssen wir uns mehr Unsicherheit zugestehen – oder wir verwerfen die Nullhypothese eben nicht. Demnach hält auch die Nullhypothese “Coca Cola und Coca Cola Zero schmecken gleich” unserem Test für die meisten Fälle stand. Und unsere letzte Challenge zeigt, dass es niemandem überzeugend gelungen ist, alle vier Marken auseinanderzuhalten.
Es lassen sich vor allem zwei Lehren aus der Geschichte ziehen. Die erste ist, dass nicht alles, was wir beobachten, so ist, wie es zuerst den Anschein hat. Stattdessen sollten wir in Betracht ziehen, dass es auch Produkt eines einfachen Zufalls sein könnte. Das tun Wissenschaftler*innen ständig wenn sie mit Stichproben arbeiten. Dabei arbeiten sie mit Zufallsverteilungen wie wir sie oben gesehen haben und stellen sich die Frage, wie sicher sie sein können, ob ein Zusammenhang wirklich besteht oder ob er nur in ihrer Stichprobe vorkommt. Dabei gehen sie immer erst davon aus, dass es keinen Zusammenhang gibt und fragen sich dann wie wahrscheinlich es ist, dass sie ihn trotzdem beobachtet haben.
Die zweite Lehre ist, dass man bei Cola viel Geld sparen kann, wenn man sich nicht vom Aufdruck auf der Flasche ablenken lässt. Die meisten, so scheint es, können keinen Unterschied zwischen einer ja-Cola und den fast viermal so teueren Marken erkennen. Aber wer weiß, vielleicht kann ein zukünftiges Experiment die Nullhypothese, dass ja- und Marken-Cola gleich schmecken, auf einem vernünftigen Signifikanzniveau in neuen Experimenten zurückweisen.